Havoc of the planetary system by the red sun | Part I: astronomy
Introduction
In this paper, we will detail a thesis on how the present state of the planetary system came apart. It will outline what happened to the solar system when a foreign star, which was surrounded by an accretion disk, crossed it there and back. Such a passage of a foreign star through the solar system may have been the cosmic catastrophe we search after to explain the accompanying and following upheaval, including the destruction of the 5th planet, the capture of the Moon by Earth and the re-melting of Venus in the course of a gigantic impact. The hypothesis of a passage of a foreign sun, which can be read from prehistoric messages, has so far only been qualitatively elaborated.
The non-reflected denial of any such thesis as a conspiracy theory is premature because it ignores the fact that celestial mechanics provides us with the mathematical instrument that can test the compatibility of the thesis with aftereffects, remaining as a disturbance on the solar system. Necessarily, the gravitational disturbances in the planetary orbits must still exist in the present. Thus, to check the plausibility of the traverse of a foreign star we compute whether the state of the planetary system can be explained as result of a gravitational distortion. In combination with the framework provided by astronomy and physics, myths, news of ancient writers, and religious teachings serve to determine the initial conditions for the celestial mechanical computations.
A major constraint develops since we find our planetary system, largely in its primordial state. From this, we deduce that the mass of the traversing star was significantly smaller than the mass of the Sun. The primordial orbits we assume to have been highly symmetrical and without any inclinations to the primordial ecliptic. Starting from this assumption we detect the perturbations by the Red Sun reflected in the shape and inclination of the planetary orbits.
If we can show, that the transformation of an initially well-ordered planetary system into its current state of recognizable disorder originates from the perturbation of an external heavy mass, this finding would not only provide indisputable proof for the existence of an external perturbator but, our model of a traversing sun would gain evidence. In case the computations yield adequate results, our model, as well as conclusions drawn, would rest on a much firmer foundation than mere guessing.
Algorithm for celestial-mechanical calculations
In Newton’s law of gravity, we find all the physics and mathematics we need for a numerical calculation of orbital perturbation. To calculate the acceleration which interacting masses exceed on each other Newton’s law of gravitation reads as:
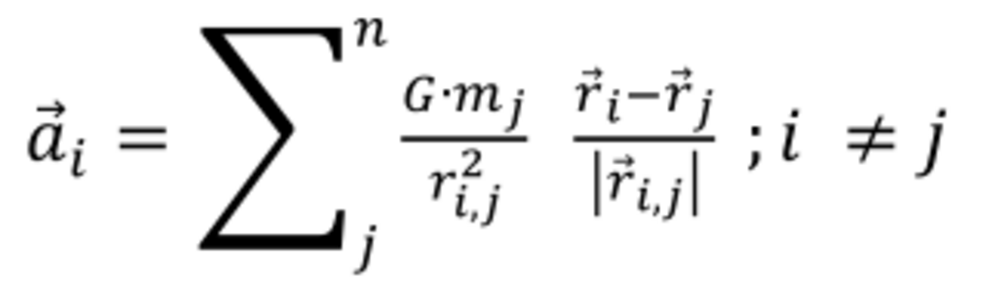
G is equal to the gravitational constant (G = 6,672428.10-11 m3/kg.s2). 𝑟𝑖,𝑗 measures the distance between the interacting mass i and mass j. For every single mass, the acceleration of that given celestial body is determined by summing up the interaction with all other masses. The summation of the accelerations overall interacting masses n provides in vector addition, the effective acceleration which the masses with running index j exert on the given mass i.
Explicitly described, the numeric practiced in the following works as follows: From the acceleration of a body i by the masses j surrounding it, we calculate the change of its velocity 𝑣⃗𝑡𝑛 and its position 𝑠⃗𝑡𝑛 for the time interval ∆𝑡 = 𝑡𝑛 − 𝑡𝑛−1 to the time 𝑡𝑛:
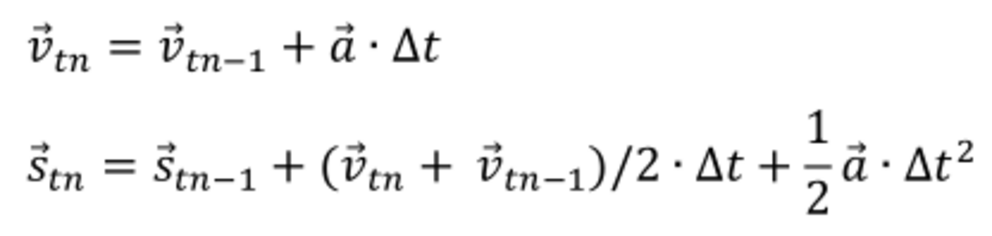
In the computations, the time interval Δt can be adjusted – depending on motion and distance – between hours and fractions of a second. This procedure can be extended by iterative repetition to any length of time. Only the value of numerical error that adds up by each iteration step limits the calculability of long-term scenarios.
Data of the initial conditions
In our computations, we assumed as the state of the solar system a primordially perfectly ordered planetary system on which the perturbator, i. e. the Red Sun, was acting. Given this choice of the initial condition, the only free parameters left for the initial conditions of each planet was its distance to the Sun and its position on its circular orbit.
A trivial limitation for the initial position and the velocity of the Red Sun results from the fact that this disrupter must penetrate deep into the planetary system. Only in this circumstance its gravitation can tilt Mercury’s orbit sufficiently strong and stretch its orbit to its present elongated ellipse. For confirmation, we find Venus, the next planet to Mercury, is second in its orbital inclination. The exceptional orbital inclinations confirm our assumptions of a close encounter between our Sun and the Red Sun. The necessity for a perihelion very close to the Sun enforces the initial condition that the intruder approached the solar system with a low transverse velocity. That is that its speed vector was almost directly pointing at the Sun. From the orbits of the outer planets, we derive another initial condition: Since at present they circle the Sun with inclinations of little variation, we conclude that their orbits are perturbated only slightly. Quantitatively, we assess the angle of incidence relative to the ecliptic from the orbital inclinations of dwarf planets, orbiting in the distance range of the gas planets. Their mere existence on these courses makes them young objects. We take them to be relics of the passage of the Red Sun and their inclinations, varying around 25° relatively to the ecliptic, as an indication for the angle of incidence of the Red Sun on its way into the solar system. At best, we can determine the mass of the Red Sun based on an educated guess. On the one hand, the mass of the interferer must be chosen significantly lower than the mass of the Sun, since otherwise, the planetary system would exist in greater disarray than it actually is. On the other hand, in order to tilt the planetary orbits and deform them into ellipses during the short period of perturbation, the mass of the Red Sun must be assumed to be significantly higher than that of a planet.
For a refined adjustment of the initial conditions, we ran iterative test calculations evaluating the perturbation effect of a dwarf sun on the planetary orbits. In particular, we paid attention to the perturbation effect on the orbit of Mercury. By this means we determined the mass of the Red Sun to be:
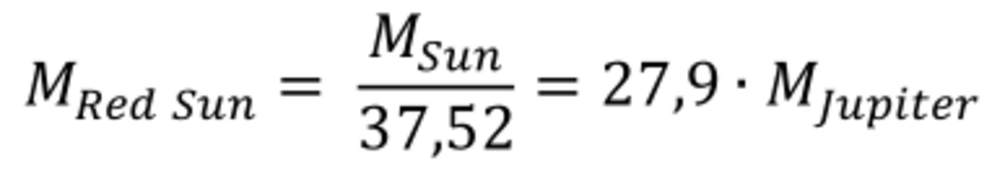
This mass corresponds to that of a small brown dwarf (surface temperature of about 2,500 K) which astronomy classifies in the spectral class L.1
The initial velocity and the chosen starting position of the Red Sun were adjusted iteratively until its gravity threw the innermost planet Mercury from the assumed perfectly circular orbit on its present orbit. At a distance of 515.9 AU (AU = astronomical unit) to the Sun the vector position of the Red Sun in a Sun-centered coordinate system was finally selected to be:
𝑟⃗0 = (466; 0; −221.3) 𝐴𝐸
This starting distance for the simulation lies well within the Oort cloud and is six times farther away from the Sun than the Kuiper Belt.
In determining the vector velocity we added the requirement that the Red Sun should cross the ecliptic close to the orbital distance of the asteroid belt and at the same time its perturbation should provide the orbital ellipticity of Mercury. To fulfil these two requirements, we determined the initial velocity to be:
𝑣⃗0 = (0; 32; −27.6) 𝑚/𝑠
Computing the path by use of these selected initial values, the Red Sun dives flatly below Earth’s and Venus’ orbit while on its path back runs far above the ecliptic.
Path of the Red Sun
The above initial conditions of mass, location and vector velocity of the Red Sun, together with the mass of the Sun – and to a negligible extent depending on the position of the planets – determine the trajectory of the Red Sun.
Given the chosen initial conditions, the orbit of the Red Sun intersects the primordial ecliptic at a 2.3 AU solar distance from north to south. (Note: the coordinate system was chosen in a way that the planets orbit counterclockwise, and the north direction is displayed to the top.) In its perihelion, the intruder approaches the Sun to a minimum distance of 0.25 AU and crosses the ecliptic plane northwards at 0.33 AU, that is while it is still moving within Mercury’s orbit. In various sections and magnifications, the graphs of Diagram 1 show the trajectory of the Red Sun.
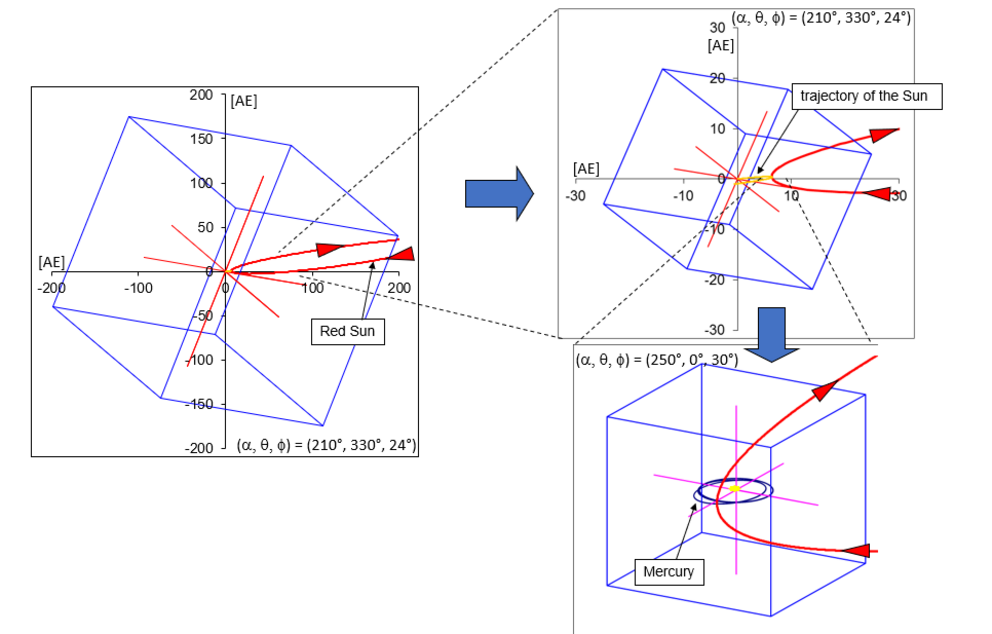 Diagram 1 Trajectory of the Red Sun (The values in the boxes are the Euler angles of the rotation of the coordinate system.)
Diagram 1 Trajectory of the Red Sun (The values in the boxes are the Euler angles of the rotation of the coordinate system.)
The mutual attraction between the Red Sun and our home Sun, whose initial position and speed in the computation have been set to zero, accelerates the two objects towards each other in inverse proportion to their masses.
The graph on the upper right shows the relative motion near the perihelion.
The graph on the right repeats, at a different scale and in the coordinate system at rest relative to the Sun, the orbital segment of the Red Sun in its perihelion. Also shown are the orbit, including the transition between these orbits, of Mercury before, during and after the passage of the foreign sun.
The cubes illustrate the position of the orbits in space with the ecliptic lying on the (x, y) plane. The angle specifications in the plots indicate the Euler angles of the respective rotation of the coordinate system.
Unexpectedly and surprisingly, the orbit of our hypothetical intruder bears a remarkable resemblance to the trajectory of Oumuamua2, a celestial body that passed through its perihelion in 2017. Oumuamua was neither an asteroid nor a comet but was identified to be of extrasolar origin. The trajectory of Oumuamua is not that astonishing because it meets the restrictions we had to make in choosing the parameters for the Red Sun. A nice and absolutely independent confirmation of the reasonableness of our selections regarding the initial conditions. As we demanded for the Red Sun, Oumuamua must have fallen towards the Sun at an absolute value of the speed as well as its speed in a transverse longitudinal direction close to zero. The simultaneous fulfilment of these criteria is by no means trivial. To assume that Oumuamua was a spy controlled by aliens is probably nonsense. Still, its trajectory raised questions when the object exited the planetary system demonstrating strange acceleration behavior on its way back to outer space. Such an acceleration was so-far unseen behavior, which is not yet understood.3, 4 Scientists with impeccable reputations are considering whether Oumuamua was an alien spacecraft.5 If this turns out true, we live at the brink of a time change.
The time sequence of the passage of the Red Sun through the planetary system, quantitatively given by measuring the time of intersecting of its trajectory with those of the planetary orbits, is shown in Diagram 2. The curvature of the curve reflects the variation of change in the velocity (acceleration and deceleration, respectively) of the Red Sun as a function of its distance from the Sun. For its flight from the outer asteroid belt (~3.4 AU) and back to this distance the flight time of the Red Sun amounts to about 7 months.
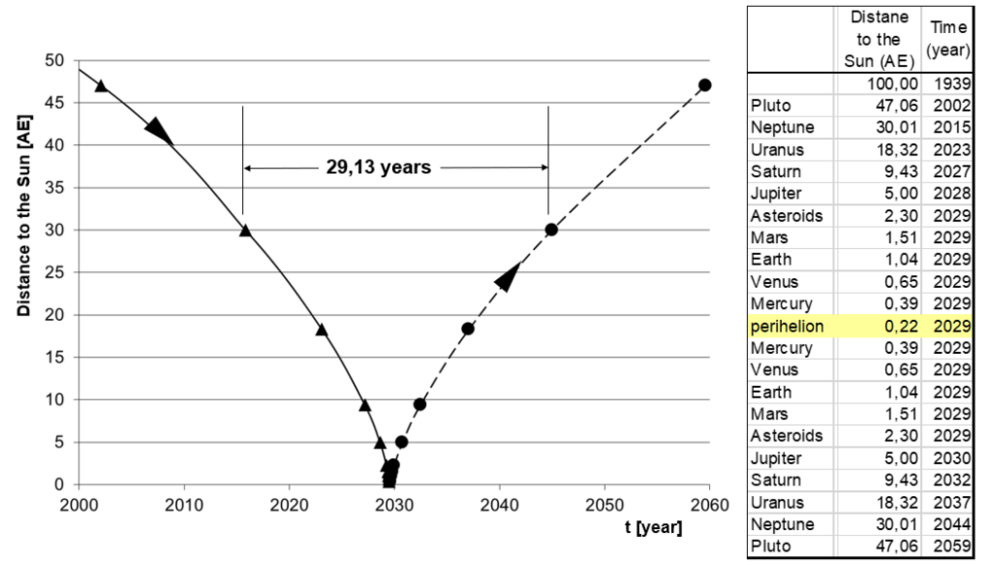 Diagram 2 Timing plot of the passage of the Red Sun through the planetary system
Diagram 2 Timing plot of the passage of the Red Sun through the planetary system
The x-axis indicates the time at which the Red Sun (in projection on the ecliptic) reaches the orbital distance of the respective planet. The time at the starting position s0 = 515.9 AU was set in the computation to t = 0.
Perturbation Effect on Mercury and Venus
The computer simulations quantified the perturbations which the Red Sun exerted on the orbit of each planet. In each of these computations two additional free parameters appear: First, the position of the planet on its orbit during the passage of the Red Sun, and second, its orbital radius before perturbation. In an iterative procedure, the position of the planet during the passage of the disturbance and the radius of its primordial orbit – deviating as little as possible from the current distance – were varied until the current orbit was sufficiently accurately approximated.
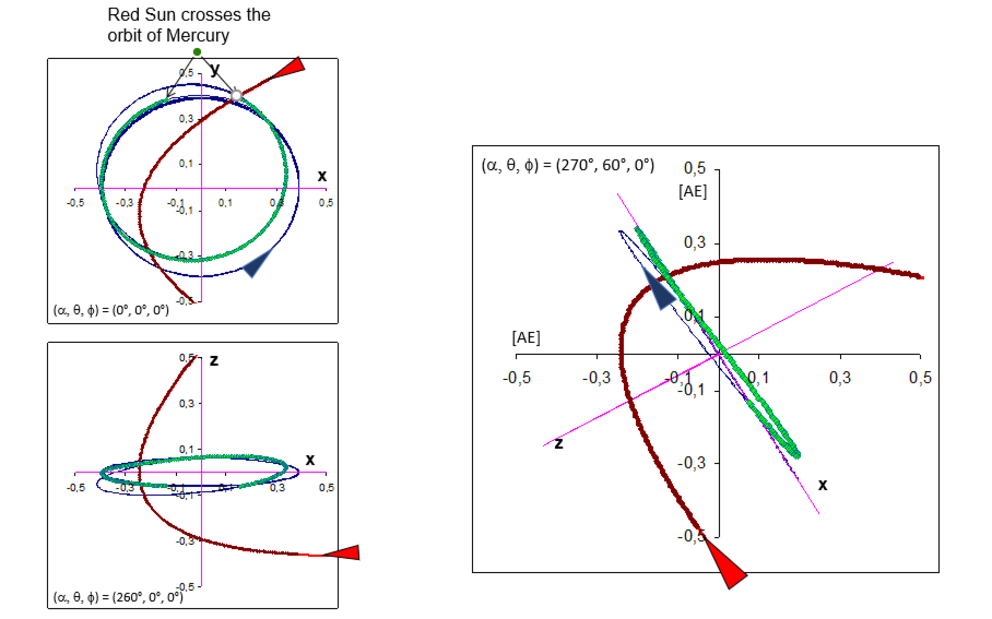 Diagram 3 Three-dimensionally animated representations of Mercury’s orbit and its changes during the passage of the Red Sun shown from different perspectives
Diagram 3 Three-dimensionally animated representations of Mercury’s orbit and its changes during the passage of the Red Sun shown from different perspectives
The curve drawn in red shows the trajectory of the Red Sun. The green segment in the path of Mercury’s orbit corresponds to the time during which the Red Sun moves within Mercury’s primordial orbit. As can be seen in the plot, Mercury runs almost a full orbit while the Red Sun resides inside its orbit radius.
The graphic illustrates not only the deformation of the circular orbit to an ellipse but also the inclination of the orbital plane.
The triplet of numbers in each graphic indicates the Eulerian angles the coordinate system was rotated in the respective perspective.
The violet axes define the axes of the main coordinate system with the (x-y)-plane in the ecliptic and the Sun at its center.
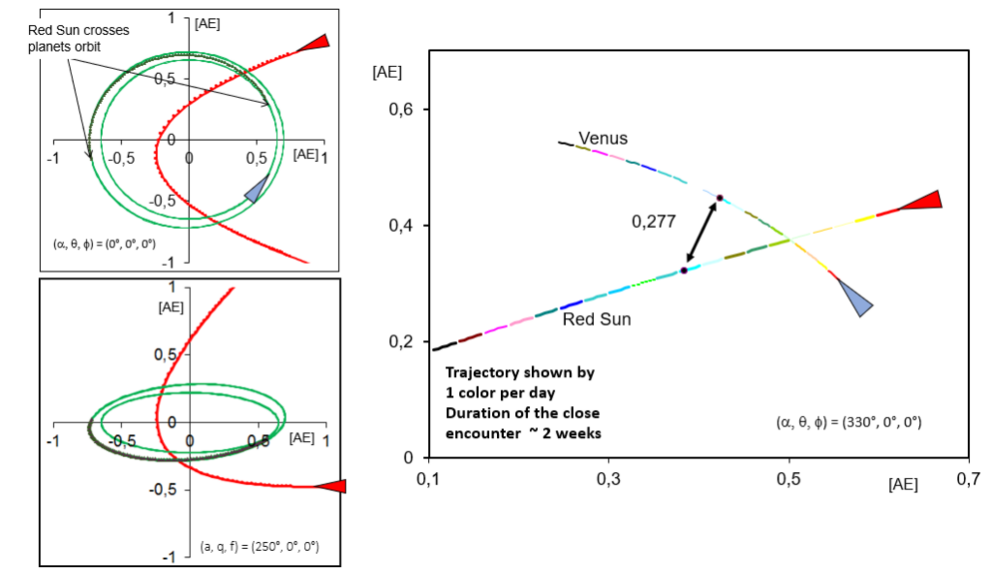 Diagram 4 Plot of the simulation results of the perturbation exerted on Venus’ orbit
Diagram 4 Plot of the simulation results of the perturbation exerted on Venus’ orbit
Shown in different perspectives and enlargements are the three-dimensionally animated orbits of Venus and the path of the Red Sun during the orbit crossing (red curve). The segments of the curves drawn bold and in darker green mark the time period during which the Red Sun moves within the distance of Venus’ orbit. The graph on the right shows the near-encounter situation on an enlarged scale. Each color marks the segment of the paths that Venus or the Red Sun, respectively, cover during a single day. The number on the double arrow indicates the minimum distance of 0.277 AU by which the two objects approach each other.
Diagram 4 reproduces the encounter constellation which led to the best adaptation of a primordial circular orbit of Venus to its present orbit. The selected constellation, in which the Red Sun traverses more or less directly beneath the planet, expands the planet’s orbit, which we assumed primordially exactly circular, into a new, again near-circular orbit and tilts it by almost 5° out of the original ecliptic. In the simulation, the current orbit of Venus – starting from a previous circular orbit – was best maintained when the Red Sun passed vertically below the planet’s position.
In view of this result, the close encounter of the Red Sun and Venus is not only an extraordinary constellation in terms of orbital perturbation, but results in an absolutely deadly event for any life on the planet, Venus. During the passing of the Red Sun, the planet is situated in the center above the accretion disk, which has turned into a gigantic hot plate. If the planet bore life until then, every organic compound in the southern Venus hemisphere was incinerated.
Planetary Orbits
Table 1 lists the primordial orbits of the planets, which were determined under the condition that the perturbation of the Red Sun transformed them into the current elliptical orbits. Furthermore, the table lists a full set of orbital data including the perihelia and aphelia of the planetary orbits, as computed in our simulations, as well as the actual data.
The calculated mean radii of the orbital distances of the planets deviate by a maximum of 0.5% from the actual values. Aphelia and perihelia are less accurately predicted by our computation. In the case of the perihelion of Venus, we ended up with a variance of 2.5% which was the largest deviation between the calculated and current values of all orbital data. For all other planets, the deviation is less than 1%. As in the case of the perihelion, the computed aphelion for Venus deviates with a difference of 1.6% – the most from the current values. As already said in the previous section the simulation of the perturbation by the Red Sun, in its need to maintain a circular orbit of Venus after the passage of the Red Sun proved to be a challenge.
However, and especially if we consider the current dynamics of the planetary system the achieved agreement can be considered as excellent. One has to note that also today the orbits of the planets are not really been frozen, although the rates of change per century in the sub-permille range are small.6 Over geological time periods these changes are by no means negligible. Consequently, it was a severely restrictive assumption to start the simulations concerning the gravity effects of the intruding sun assuming perfect circular orbits. In spite of these long-term variations, we consider it reasonable to assume orbits close to circles since this most likely reflects their primordial genesis. Secondly, resonances stabilize the orbital times of moons and planets on circular orbits, at least keep them close to circles. The dynamics of a given orbit is featured by a positive feedback. As a rule of thumb, the more elliptical the orbit is, the stronger the mechanism rounding the orbit into a circle.
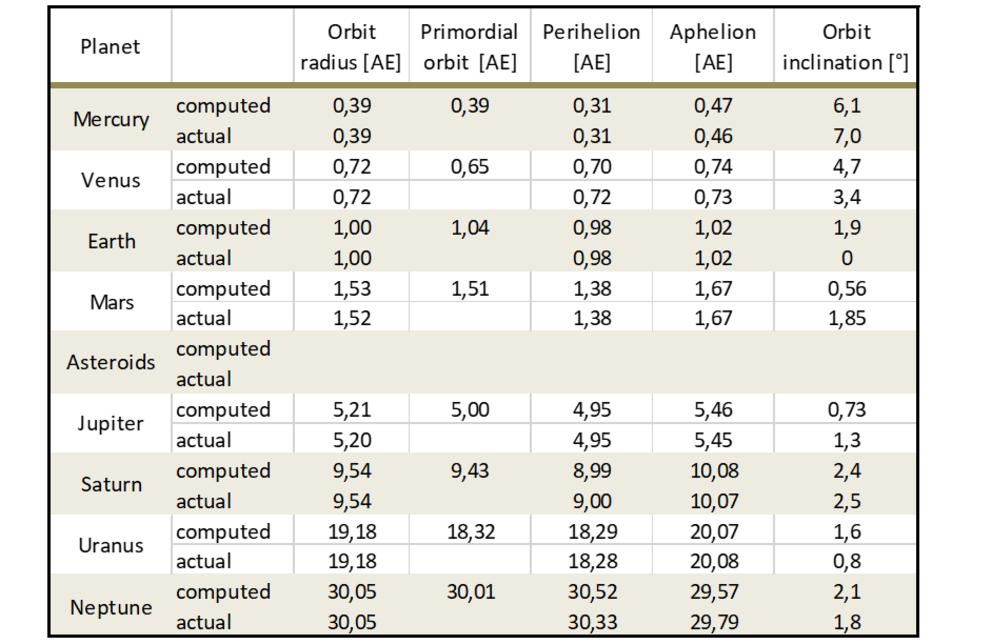 Table 1 Compilation of orbital data of the planets (computed and measured)
Table 1 Compilation of orbital data of the planets (computed and measured)
The first data column lists the current orbit distance of the planets.
The second column shows the primordial orbital distances as selected for the computer simulation prior to the perturbation by the Red Sun.
The last three columns display for each planet the calculated and the current data of its perihelion, aphelion and orbit inclination.
The Inclination of the Planetary Orbits
Confidence in the validity of our computer simulation and its informative value would increase if the computation would not only provide the geometry of the planetary orbits but also their inclinations. As said, the shape of the current orbit was a decisive criterion for the choice of the primordial orbit of a certain planet. The current orbital inclination, on the other hand, was not. If we find the calculated data in agreement with the actual inclination, we achieve a plausibility of proof. We would achieve even more than plausibility, if we have obtained the orbital inclinations as a side result our computations are correct. To find this concurrence comes close to proof of the factual accuracy of our model.
A look at the ring system of the planet Saturn shows how poorly the inclination of the planetary orbits complies with the model of planet formation from a primordial accretion disk. If we choose the thickness and planarity of Saturn’s ring (exhibiting 1 million km in diameter it is less than 1 km thick) as the model for the accretion disk out of which the Sun and the planets formed, we expect for no planet any inclination at all. In fact, if the Sun’s primordial accretion disk was as flat as Saturn’s rings, this leads to orbital inclinations of millionths of an arc degree – i.e. not by factors, but by orders of magnitude smaller than those inclinations we observe in today’s solar system. In view of the planarity of an accretions disc, it’s hardly surprising large moons orbit their parent planets with minimal orbital inclinations.
Since in a perfectly planar system there are no torques for lifting the orbits out of the plane, we can exclude internal interactions as a cause for the different orbital inclinations of the planets and have to assume an external perturbance, that is an external force acting. No chaos theory can overturn this logic of physics. The situation, which is astonishing from a mechanical point of view, has already tempted great minds to wild speculations. Newton, Johann Heinrich Lambert and other scientists of the 18th century went so far as to attribute the (dis)order of the planetary orbits, and here above all the different inclinations of the orbits, to the work of God. They even speculated that this incomprehensible fact represents a proof for the existence of God. Maybe, the assumption of an external perturbator offers a more genuine alternative.
Checking the match of calculated inclinations with present-day inclinations is not a trivial matter to be immediately read off from the simulation results, but beforehand various effects must be considered.
The Red Sun inclined the orbits of all planets against the primordial ecliptic, including the orbital plane of Earth. At present, however, Earth’s orbit is chosen as the plane of reference. The use of this reference instead of the hypothetical primary ecliptic affects the inclination angle of all other planetary orbits. The 1.9° by which the Red Sun has tilted Earth’s orbit out of the primordial ecliptic we find reflected in the orbital inclinations of the other planets. Since the outer planets never came close to the Red Sun and its trajectory run far above their orbits, these were only slightly tilted against the primordial orbital planes. The small inclinations they exhibit will therefore largely be a consequence of the inclination of the orbital plane of the Earth afterwards chosen for reference.
Furthermore, when analyzing the orbital inclinations of the planets, it must be borne in mind that the apses rotate. As a result of the rotation of the apses of Earth’s orbit the inclinations of all the other planets will reduce and increase depending on the relative position of the orbital nodes. (orbital node = point at which due to other inclination the planetary orbit intersects the ecliptic). If the orbital nodes of Earth and planet happen to be at the same angle, the inclination measured versus Earth orbit becomes minimal. However, when they are opposite at a 180° difference, orbital inclination is maximal. Since the angles between the nodes are not fixed in space, the value of inclination is not constant but dynamic.
The rotation is caused by the gravitational interaction of the planets among each other. In addition, relativistic corrections in the gravitational field of the Sun makes a small effect on the rotation of the line of apses (= major axis of the orbital ellipse) of the inner planets. (This effect became famous, because it served as proof of the general relativity theory. The effect predicted by Einstein’s theory clarified a classically unexplainable residue in the perihelion (apsis) rotation of Mercury).
The apses rotate at an angular velocity that is given in degrees per century. This is not that slow as it does not even require geological time periods for this correction to become relevant. The ellipse of the Earth’s orbit rotates at 0.323° per century, 8 so it takes about 111,500 years for one full rotation. The rotation of the Earth’s apsidal line superposes the faster precession of the Earth’s axis, which makes a 360° rotation during a Platonic year of 25,780 years. However, precession is not afflicting the orbital plane. Different to apsidal rotation the slow spinning of Earth’s axis isn’t caused by the force of other planets, but by the torque exerted on the flattened body of the Earth by the much stronger gravitational forces of the Moon and the Sun. 9
As the precession of Earth’s axis does, the rotation of the orbital ellipse leads to a change in the position of the stars in the sky. Timewise the apses rotation results in small changes in the starry sky compared to the change of the firmament due to the gyroscopic movement of Earth’s axis.
The consecutive temporal lifting and lowering of the orbital plane of the planets is a function of the differences in the angular velocities at which the apses of the Earth and the planet rotate relatively to each other. As just explained using the example of the two extreme positions of the relative positions, different speeds of rotation of the nodes lead to a changing inclination of a planetary orbit against the plane of Earth’s orbit thus against the reference orbit. As a result of the different rotation speeds, in some cases even in opposite direction of the orbital ellipses, the inclinations of the planet orbits seemingly wobble.
According to our simulation result concerning the inclination of the Earth’s orbit and as a result of its choice as a reference plane the orbits of the other planets over time tilt continuously up and down by 1.9°. With the Earth’s orbit employed as a reference plane, over time the orbital inclinations of the other planets vary by 3.8° around the angle of inclination of which the gravity of the Red Sun lifted the specific planet out of the primordial ecliptic.
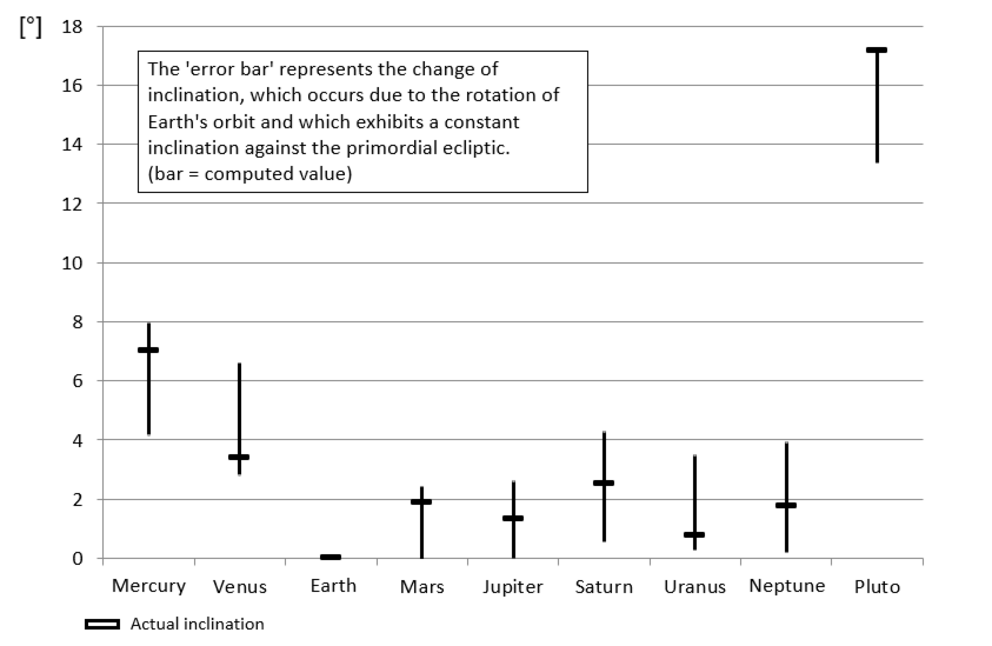 Diagram 5 Variation of orbit inclinations of the planets as a function of time
Diagram 5 Variation of orbit inclinations of the planets as a function of time
The apsidal rotation of the Earth’s orbit causes the inclinations of the other planetary orbits to wobble by +/- 1.9 degrees (indicated by the length of the vertical bars). The middle of the vertical bars corresponds to the inclination angle, which originates from the passage of the Red Sun.
The bold horizontal bars represent the current orbit inclination relative to the orbit plane of Earth.
Chronological classification
Our consideration of the variation of the orbital inclinations simplifies the problem and represents a lower estimate of the full problem because it neglects the torques which the planets exert on their inclined orbits among each other. However, if we maintain the assumption that the passage of the Red Sun took place in prehistoric times, i.e. geologically recently, we can justifiably neglect changes in orbital parameters as predicted by chaos theory. Therefore, for proof of our model, we consider only the 1.9° inclination of the Earth’s orbit and its rotation to be relevant. As shown in Diagram 5 the agreement of the simulation values with the real orbit inclinations is satisfactory to good. We note: No orbital inclination is outside the interval that predicts the variation in inclination due to the apsidal rotation of the Earth and the planet.
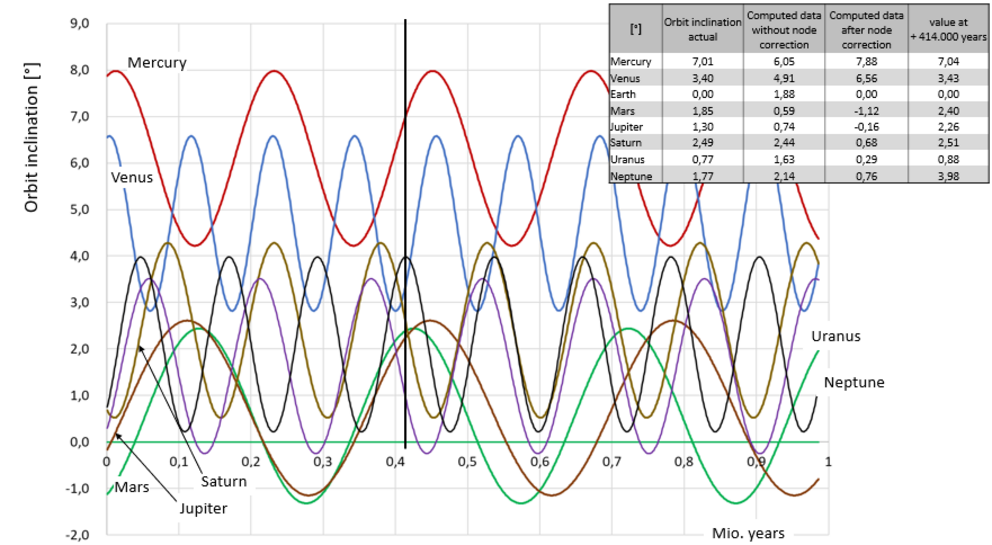 Diagram 6 Variation of the inclination angles of the planetary orbits over time as a consequence of the inclined orbital plane of the Earth and the rotation of the apsidal line
Diagram 6 Variation of the inclination angles of the planetary orbits over time as a consequence of the inclined orbital plane of the Earth and the rotation of the apsidal line
The values at t = 0 correspond to the orbital inclinations as calculated (see also Table 1). The curves represent the changes of orbital inclination of each planet assuming the rotation speed is constant. Because the orbit of Venus is nearly a circle, the apsidal line of Venus rotates extremely slowly at 0.005°/century. Therefore, the periodicity of the inclination of Venus’ orbit essentially reflects the rotational speed of the Earth’s orbital inclination.
Starting from our computation result of initial inclination and node position the best match with today’s values is shown in Diagram 6 by the vertical line at 0.414 million years. At this point, the orbital inclinations of Mercury, Venus, and Saturn fit quite well at this time, data deviations in the case of Mars and Uranus look tolerable, whereas the respective deviation for Jupiter and Neptune is large. This back-calculation probably exceeds the meaningfulness of our simulation. In particular, the position of the node after the passage of the Red Sun is a critical value and too sensitive to truly rely on it in the perturbation result. In addition, because the current rotational speed of the apses is not a constant, but varies with the ellipticity of the orbit, which itself is a function of time. In addition, the inclinations of the planetary orbits in question rotate comparatively fast, so that even small adjustments in the rotational speed inflict the results.
Someone who owns a fast computer and is willing to invest enough time can calculate another set of orbital inclinations and find out by trial and error which foreign star of which mass on what trajectory yields the data which comply with his hypothesis when the event took place. However, before you start with determining the date from the inclinations of the planet orbits make sure your orbit data correspond to their actual paths.
Isotope Anomaly
Is there any more solid evidence than that provided by the orbital data? In fact, there is. In the Earth’s crust, quite near to the surface radioactive isotopes were found, whose half-life excludes that they already were present in the primordial accretion disk out of which Earth formed.10 Both isotopes iron 60 (60Fe) (half-life 2.6 million years) and plutonium 244 (244Pu) (half-life 80 million years) must have been deposited far later. From the data, scientists conclude that the elements were created less than 10 million years ago in a supernova explosion. Probably the Red Sun surrounded by accretion disc formed in the cloud of fresh stardust. As these isotopes are found in measurable quantity on Earth an accretion disk becomes a likely source. In a sense, the accretion disk acted as a transport vehicle. Whilst traversing the solar system, the disc disintegrated and built a cloud which in turn was and is the source of freshly created isotopes. All this is a different story which we will outline in a subsequent article. In any case, the traverse of the Red Sun finds in the occurrence of short-living isotopes an unexpected and completely independent confirmation.
Summary
Inspired by news and myths from prehistoric times, we simulated the passage of an alien dwarf star through the planetary system. We call it the Red Sun. The computation results provide an excellent explanation for the disorder of the current state of the planetary system. Before the passage of the Red Sun, the primordial solar system had taken the harmony of a settled state. Supposing the passage of the Red Sun, we found a starting event that may explain other oddities and recent upheavals in the mechanics of the planets of the solar system.
Regardless of the daring estimation of the time at which the Red Sun crossed the planetary system the computed data basically support the reasonableness of our model. The simulation of the perturbations caused by the Red Sun not only yields the correct ellipticity of the orbits of the planets but also provides a satisfactory description of the current values of the inclinations of the planetary orbits. We consider our model yields a more convincing and straightforward explanation than chaos theory. In particular, the hypothesis of the passage of the Red Sun leads a way to explain the origin of the Asteroid Belt, the mechanics and climate of Venus, and to answer the question of why the Earth only came to have its Moon in the geologically recent past.11
We will devote ourselves to these aftermath processes and related myths in following articles.
For full references please use source link below.